다익스트라?

엄청난 분이시다... 다익스트라 알고리즘을 개발해서 최단경로 문제도 연구하시고
세마포어도 이 분께서 처음 연구하셨다고..!
그럼 간단하게 다익스트라 알고리즘에 대해서 알아보자.
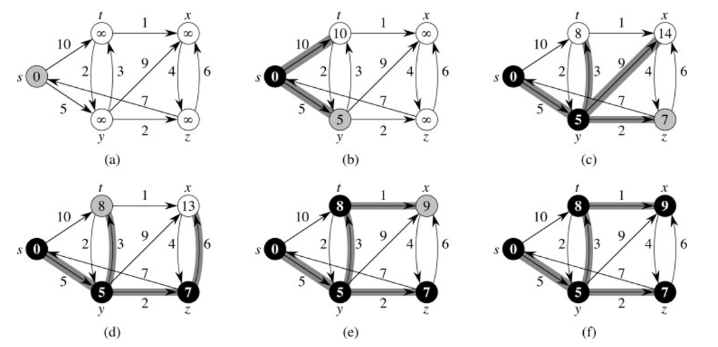
다음과 같은 그래프가 있다고 하면, s에서 다른 노드로 가는 최단거리를 구하려면
1. 바로 갈 수 있는 노드는 그 거리를 저장하고, ( t = 10, y = 5 ) 직접 이어지지 않았다면 거리를 무한으로 저장한다.
2. 갈 수 있는 가장 가까운 노드(y)에서 다른 노드까지 직접 가는 거리를 더해서 만약 작다면 갱신해준다.(t = 10 -> 8 )
3. 또 s에서 (다른 노드를 거치든 안 거치든) 가장 가까운 노드 (z = 7 , t = 8이므로 z )에서 다른 노드간 거리를 합해서 최단 거리를 갱신한다
4. 반복해서 모든 노드까지 가는 최단거리를 구한다.
코드로 보자.
INF = int(1e9)
def dijkstra_naive(graph, start):
def get_smallest_node():
min_value = INF
idx = 0
for i in range(1,N):
if dist[i] < min_value and not visited[i]:
min_value = dist[i]
idx = i
return idx
N = len(graph)
visited = [False] * N
dist = [INF] * N
visited[start] = True
dist[start] = 0
for adj, d in graph[start]:
dist[adj] = d
for _ in range(N - 1):
cur = get_smallest_node()
visited[cur] = True
for adj, d in graph[cur]:
cost = dist[cur] + d
if cost < dist[adj]:
dist[adj] = cost
# O(N^2) 시간복잡도
return dist
위 코드는 for문을 두번 돌기 때문에, 시간복잡도가 O(N^2) 이다. 노드의 수가 많아질 수록, 기하적으로 연산횟수가 많아질 것.
그래서 우린 우리가 배운 자료 구조 중 하나인 힙(Heap) 을 이용할 것이다.
import heapq
INF = int(1e9)
def dijkstra_pq(graph, start):
N = len(graph)
dist = [INF] * N
q = []
heapq.heappush(q, (0, start))
dist[start] = 0
while q:
acc, cur = heapq.heappop(q)
if dist[cur] < acc:
continue
for adj, d in graph[cur]:
cost = acc + d
if cost < dist[adj]:
dist[adj] = cost
heapq.heappush(q, (cost, adj))
return dist
힙 구조는 자료를 빼고 넣는데 O(logN)의 시간이 들기때문에 for문에서 O(N), heappush에서 O(logN)이라서 O(N log N )의 시간복잡도를 가지고, 이는 O(N^2) 보다 훨씬 적다!
화성탐사
자료출처 : 이것이 코딩테스트다 with 파이썬, 나동빈 저
입력을 그래프로 받는데, 이때 graph[0][0]에서 graph[n-1][n-1] 까지 이동하는 최단거리를 구하는 문제였다.
dx, dy를 이용해 현재 행, 현재열의 거리 + 다음 행렬까지 가는 거리의 합이 저장된 행렬까지 가는 거리보다 짧으면 갱신해주는 식으로 dist배열에 저장해서 끝까지 계산해준다.
import heapq
INF = int(1e9)
T = int(input())
def mars(graph):
dr = [1,0,-1,0]
dc = [0,1,0,-1]
N = len(graph)
dist = [[INF] * N for _ in range(N)]
q = []
dist[0][0] = graph[0][0]
heapq.heappush(q, (graph[0][0], 0, 0)) # 누적비용, row, col
while q:
acc, r, c = heapq.heappop(q)
if dist[r][c] < acc:
continue
for i in range(4):
nr = r + dr[i]
nc = c + dc[i]
if 0 <= nr < N and 0 <= nc < N:
cost = dist[r][c] + graph[nr][nc]
if cost < dist[nr][nc]:
dist[nr][nc] = cost
heapq.heappush(q, (cost, nr,nc))
return dist[N-1][N-1]
for _ in range(T):
N = int(input())
graph = []
for __ in range(N):
graph.append(list(map(int, input().split())))
print(mars(graph))가장 싼 항공기
https://leetcode.com/problems/cheapest-flights-within-k-stops/
Cheapest Flights Within K Stops - LeetCode
Can you solve this real interview question? Cheapest Flights Within K Stops - There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to
leetcode.com
우선순위 큐를 이용해서 플었는데, 노드의 수가 많으니까 timeout이 뜬다...
어던 부분에서 더 최적화 할 수 있을 지 모르겠으나, 일단 지금까지의 풀이를 적어놓고 나중에 다시 풀어봐야겠다.
import collections
import heapq
from typing import List
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
graph = collections.defaultdict(list)
# 그래프 인접 리스트 구성
for u, v, w, in flights:
graph[u].append(v, w)
# 큐 변수 : [(가격, 정점, 남은 가능 경유지 수)]
Q = [(0, src, k)]
# 우선순위 큐 최솟값 기준으로 도착점 까지 남은 최소 비용 판별
while Q:
price, node, k = heapq.heappop(Q)
if node == dst:
return price
if k >= 0:
# 그래프에 이어져 있는 원소들과 연결 했을 때
for v, w in graph[node]:
# v를 거쳐갈 때의 비용을 추가해서 힙에 넣음
alt = price + w
# 일단 힙에 넣은 다음에 나중에 pop될 지는 모름!
heapq.heappush(Q, (alt, v, k-1))
return -1
오늘 회고
다익스트라 알고리즘 자체는 어느정도 들어봐서 알고있었지만, 이를 코드로 구현하는 것에서 어려움이 많았다. 다시한번 손으로 짜보면서 익숙해져야겠다.
'항해99 > [항해99] 알고리즘' 카테고리의 다른 글
| [항해99] DP - Dynamic Programming (0) | 2023.12.30 |
|---|---|
| [항해99] 최단경로 찾기 - 플로이드 (0) | 2023.12.30 |
| [항해99] 이진탐색 - 2 (0) | 2023.12.27 |
| [항해99] 이진탐색 (0) | 2023.12.27 |
| [항해99] 정렬 ( quick, merge) (0) | 2023.12.25 |
